反傳遞演算法 -- 計算案例

為了講清楚反傳遞算法，我們必須先發明一點數學符號！

讓我們先回頭看看梯度中的基本元素，也就是偏微分，其定義是：

$\frac{\partial }{\partial x_i} f(x) = \lim_{h \to 0} \frac{f(x_1, ..., x_i+h, ...., x_n)-f(x_1, ..., x_i, ...., x_n)}{h}$

舉例而言，假如對 $f(x,y) = x^2+y^2$ 這個函數而言，其對 x 的偏微分就是：

$\frac{\partial }{\partial x} f(x,y) = \lim_{h \to 0} \frac{f(x+h,y)-f(x,y)}{h}$

而對 y 的偏微分就是：

$\frac{\partial }{\partial y} f(x,y) = \lim_{h \to 0} \frac{f(x,y+h)-f(x,y)}{h}$

以上的數學符號源自《萊布尼茲》

簡易案例

讓我們考慮一個兩層式網路如下圖，該網路是計算 f = (x+y) * z 這個算式。

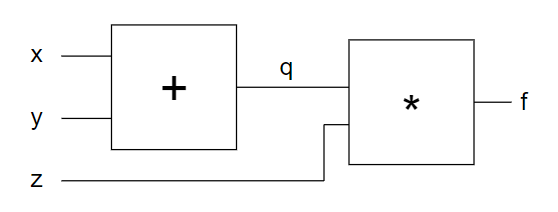
其中的 q = x+y, 而 f = q*z。

反傳遞的原理主要來自偏微分的鏈鎖規則，我們可以用以下數學式描述 f, q, x 之間的梯度關係。

$\frac{\partial{f(q,z)}}{\partial{x}} = \frac{\partial{q(x,y)}}{\partial{x}} \frac{\partial{f(q,z)}}{\partial{q}}$

但是其中的 ${\partial{x}}$ 並非偏微分，而是 $\frac{\partial{f(q,z)}}{\partial{x}}$ 才是 f 函數對 的偏微分，這樣寫起來不僅冗長，而且會引導我們一直去把 ${\partial{x}}$ 想成偏微分 (梯度向量的其中一個軸)，因而會造成很多誤解！

為了避免誤解，我們採用 $g^x_f=\frac{\partial{f}}{\partial{x}}$ 這樣的表達形式，於是可以有下列偏微分式：

$g^x_f=\frac{\partial{f}}{\partial{x}}$

$g^y_f=\frac{\partial{f}}{\partial{y}}$

$g^q_f=\frac{\partial{f}}{\partial{q}}$

$g^z_f=\frac{\partial{f}}{\partial{z}}$

然後我們可以改寫鏈鎖規則成為以 g 為主的形式：

萊布尼茲形式 : $\frac{\partial{f(q,z)}}{\partial{x}} = \frac{\partial{q(x,y)}}{\partial{x}} \frac{\partial{f(q,z)}}{\partial{q}}$

以 g 為主的形式: $g^x_f = g^q_f * g^x_q$

這樣的畫我們就可以寫出下列兩組關係式：

$g^x_f = g^q_f * g^x_q$

$g^y_f = g^q_f * g^y_q$

由於 f=q*z, q=x+y ，因此我們可以計算出下列算式：

$g^q_f = z$

$g^x_q = 1$

$g^y_q = 1$

所以我們得到

$g^x_f = g^q_f * g^x_q = z * 1$

$g^y_f = g^q_f * g^y_q = z * 1$

如此只要把 z 值帶入就能計算出梯度 $g^x_f$ 與 $g^y_f$ 了。

透過這種方式，我們可以一層一層的算回去，得到 f 對任意變數的梯度。

更複雜的案例

$f(x,y) = ((2*x)+(y+1))^2$

在 x=3, y=2 時，正向傳遞後再反向傳遞的結果為：

運算式	正向傳遞	閘的梯度	反向傳遞
x = 3	p=6	$g^x_f = ??$	36
y = 2	p=6	$g^y_f = ??$	18
p = 2*x = 2x	p=6	$g^x_p = 2$	$g^x_f = g^p_f*g^x_p=18*2=36$
q = y+1	q=3	$g^y_q = 1$	$g^y_f = g^q_f*g^y_q=18*1=18$
r = p+q = 2x+y+1	r=9	$g^q_r = 1$ ; $g^p_r = 1$	$g^q_f = g^r_f*g^q_r=18*1$ ; $g^p_f=g^r_f*g^p_r=18*1$
$f = r*r = (2x+y+1)^2$	f=9*9	$g^r_f = 2r=18$	$g^r_f = g^r_f*g^f_f=18$
f = f	f=81		$g^f_f = 1$

2x  => p
       + => r*r => f
y+1 => q

$g^x_f = g^r_f * g^p_r * g^x_p = 1*18*2=36$

$g^y_f = g^r_f * g^q_r * g^y_q = 1*18*1=18$

檢驗:

正向: $f(x,y) = ((2*x)+(y+1))^2 = (2*3+2+1)^2 = 9^2 = 81$

反向:

$g^x_f = 8x + 4y + 4 = 8*3 + 4*2 + 4 = 36$

$g^y_f = 4x + 2y + 2 = 4*3 + 2*2 + 2 = 18$